The Rookery

"Base times height" "One half base times height" These are the formulas for the area of a parallelogram and the area of a triangle respectively.  Even if you haven't bought carpet for a triangular room recently, they're probably rattling around in your brain somewhere.  What might not still be rattling around was how confusing the ideas of area and perimeter are initially.

Fourth and fifth graders understand perimeter but the idea of measuring surfaces is new.  "Squareinches" are very literal.  A part of a square?  Well, that must not count.  How could you measure a triangle in squares?  The confusion is compounded when you start thinking that squares could be feet, meters, miles…Often, it's the kind of thing that makes sense when they're doing it (on a worksheet, for example) but then, when they try to apply it in a new situation, they stumble.

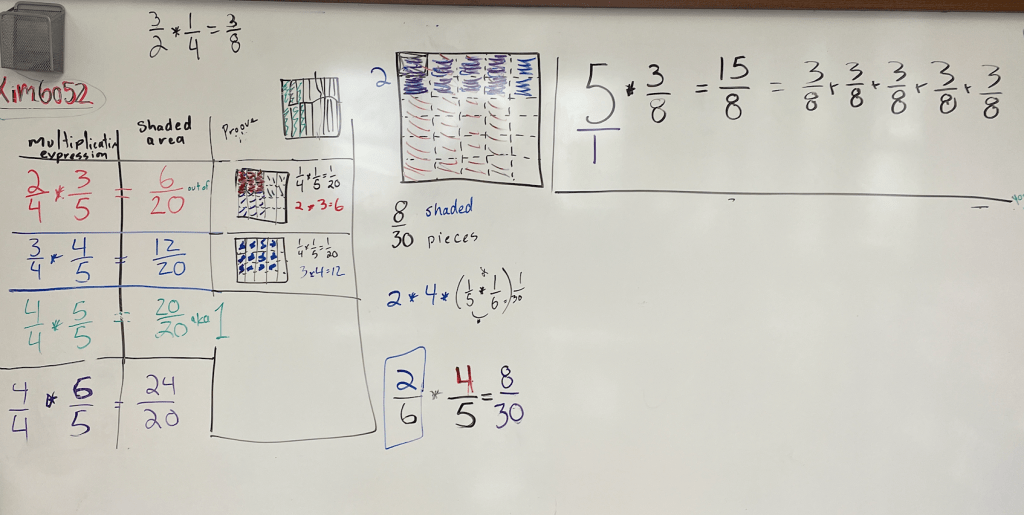
From a teaching perspective, it can be frustrating.  According to the worksheets we did from Everyday Math, everyone's understanding was coming along nicely.  We took parallelograms and turned them into rectangles, thus "discovering" the formula for a parallelogram.  Then we took identical triangles, turned them into parallelograms and "discovered" the formula for a triangle.  These are activities I chose from that particular curriculum because they are very concrete but lead students along toward an abstract understanding.

But those worksheets weren't enough.  When I went to a new application, many students didn't use the formulas which had seemed so solid the day before.  Instead, they tried drawing in squares to figure out the area or they used the perimeter and cut in in half "because, well, I remember it's half of something." 

It's an illustration of why I don't feel that a single math curriculum is the answer to teaching mathematics.  Each curriculum has its own strengths but also its limitations.  The Herons were able to do area the way it was presented in Everyday Math — but they weren't able to then apply it in a new situation.  Had we just worked within the structure of Everyday Math, the superficiality of their understanding (please excuse the generalization) would not be apparent.  

After the mini assessment I did, I saw that many kids are still struggling with the idea of arrays and how they're related to a shape's measurements.  They can apply the formula when they're told to use it — but they don't have the fundamental understanding necessary to see how the formula works and therefor when it is applicable.

I have the opportunity as a math teacher to choose from among many resources to meet the Herons' needs.  Next, I'm going to turn to some explorations that connect the abstract to the concrete and really force them to consider how perimeter and area are connected (or not connected).

Here is some video of a lesson where we were trying to find as many shapes as we could where the area was 24 squares.