 So, as I right this, Prairie Creek's two student teachers are at my board, coloring in squiggly designs. Why?
So, as I right this, Prairie Creek's two student teachers are at my board, coloring in squiggly designs. Why?
As soon as we got back from Babe (which was a lot of fun), I settled the Herons down for some more discrete math work. This Friday, at our faculty professional development day, I'll be leading a workshop about devleoping a child's sense of wonder in mathematics. The Herons were my guinea pigs for one of the lessons.
We had recently made simple closed curves that could be colored with just two colors. The rules for the coloring were simple: two shapes that shared an edge could not share a color. They are allowed to  touch at a vertex as long as they don't share an edge.
touch at a vertex as long as they don't share an edge.
Today we expanded the challenge. The Herons could create any design, ANY DESIGN, and there would be a way to color it in with just four colors. Could they find one that necessitated 5?
Three felt they had. Their designs are on this page. You can print them out (click for a full size image) and give it a try or make up your own and send it in for the Herons to try. What's your technique for coloring? Does it matter where you start? How could ANY design work? Does it have to be flat? How does making it three dimensional change the game? These are real questions for real mathematicians. They are also a lot of fun. 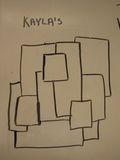




Leave a comment