One of my favorite memories of teaching math at Prairie Creek came during a lesson on area that conincided with Village. A student came up to me and said, "Thanks Michelle! I really needed that." It's the highest praise a progressive teacher can receive. We are constantly trying to make students' work feel real — we try to create an imperative, a need for what they are learning.
In Village, students design their own houses to 1/24 scale. They plan their house and then have to fill out a wood order form which details each piece they will need and gives its area and cost (wood is priced by the square mini foot (square half inch).
This year, we are allowing students to begin planning their houses now. They can even fill in their order forms. But they also have to do all of the math to find the area of each piece of their house.
For many, this has meant doing a lot of work discovering how area works, developing a formula for finding the area of parallelograms and triangles and then using those formulas enough to feel confident with them. After all, one wouldn't want to get the area of one's roof wrong and have to, gulp, order and pay for a new piece.
Students have been busily creating parallelograms, cutting them at a right angle to the base and "proving" that base times height gives one the area of any parallelogram. We then created two congruent triangles and used them (and several more sets) to "prove" that every triangle can be doubled to create a parallelogram and, therefor, base times height divided by two gives one the area of a triangle. We will practice this a lot and then apply it to our peep houses.
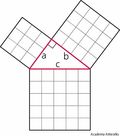
The students who have already had a lot of experience with area have been working to use algebra to figure out the height of the triangles they need for various pieces. I taught them the basics of the Pythagorean theorem and they have been using it to determine the length of the roof they need or the height of their peaks. Some students are building unusual and complicated houses that require a lot of this kind of ciphering. I'm also refusing to check their work for accuracy so they are relying on each other to check work (and debate various approaches to solutions.)
Don't worry, I'll show the Pythagorean theorem to those students who are focusing primarily on area. However, I won't expect them to apply it by themselves this year. Instead, I will talk through my work as we use the theorem to figure out the initial dimensions of their house. It's a great opportunity to share one of those pieces of math that can instill a lot of wonder and awe. They don't have to understand it completely to find it amazing.





Leave a comment