The Rookery

This week in our exploration math workshops, we're working on solidifying algorithms.  We throw around the word "algorithm" a lot.  Simply put, an algorithm is a step by step method for doing something.  In math, it's a way to keep track of computations that are too complex to do in our heads.

In order to be ready to learn an algorithm, a student has to have a solid understanding of the concept of the given operation.  A multi-digit multiplication algorithm will make no sense to a child who has not yet really grasped that multiplication is the combination of same size groups.  They may be able to memorize the steps but they will not use the algorithm independently to solve problems.

The group I'm teaching is working on long division algorithms.  The algorithm I begin with is modified so that one doesn't have to be as precise when figuring out how many of the divisor "fit" into a given number.  You can creep into the answer by small increments.  You're not wrong, you're simply not as efficient.  The traditional algorithm, by contrast, is rather unforgiving.  If you under estimate the number you have to erase because you're "wrong."  The traditional algorithm is best for students who really, really know their facts.  For students who have great mental subtraction skills, there's an even better algorithm called "long division short."  Why not just learn one algorithm?  Well, once kids really understand what's going on, all the algorithms make sense — by comparing where all the numbers go in different algorithms, they get a much deeper understanding of what they're really doing and why.  This is at the heart of math that students can use and extend.  It's also at the heart of the new Common Core standards (here's a great article about the common core and math thinking)

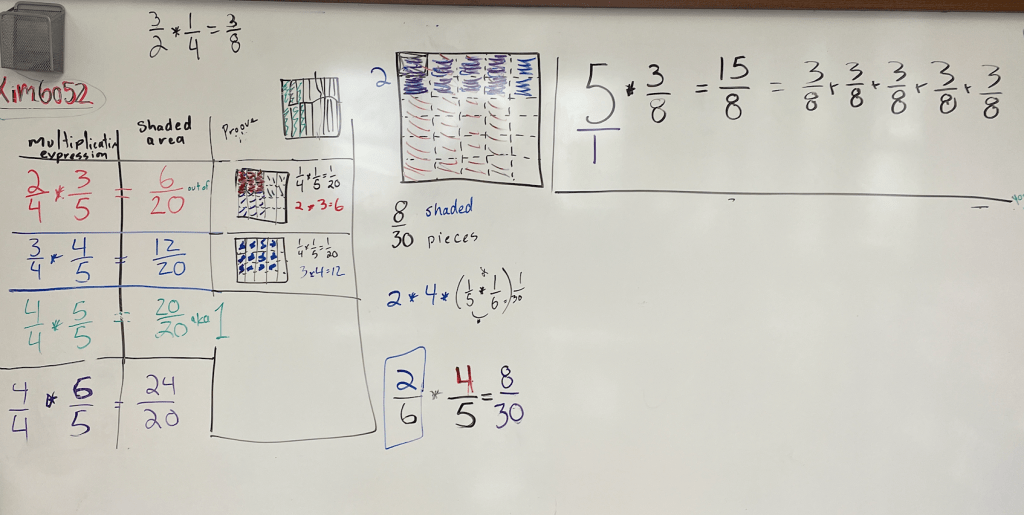
Today, while I was teaching one group the 1st algorithm, I was working with a second group who could do all of the algorithms without error.  I challenged them to think about what it meant to divide by a fraction.  Because their understanding of division was strong and deep, they could use the algorithm they knew to explore this new concept.  They quickly shared with me their discovery that when they divided by 1/4 it was the same as multiplying by 4!  "Wait" C.N. said, "What do you do if it's a fraction like 3/4 and it has a number that's not one as the numerator?"  The group quickly tackled that problem, again, using what they knew about division.

Want to see the algorithms in action?  I've made a series of videos that explains each one step by step.  The second video in the list explains why we use this algorithm as a starting place instead of just doing the "traditional" long division algorithm: