The Rookery

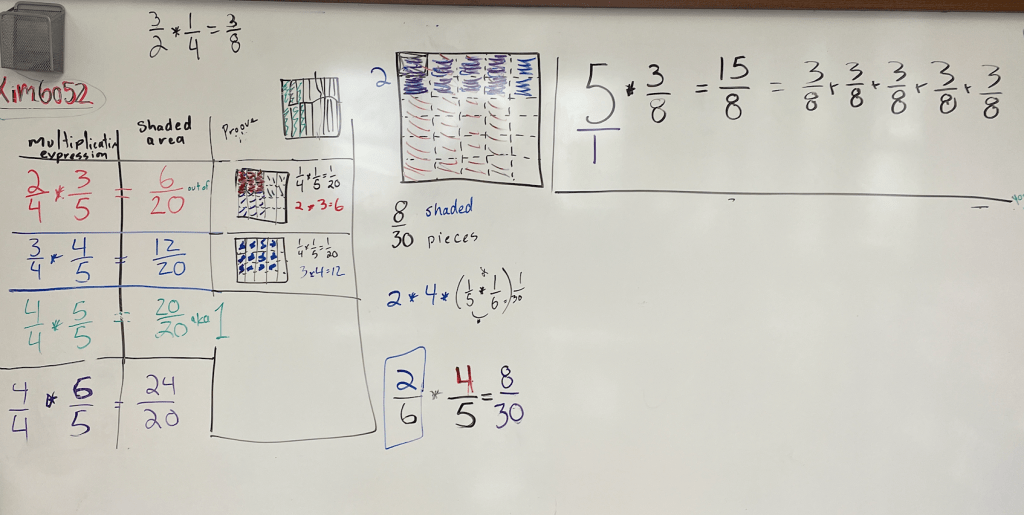
“I really don’t get why 2/5 times 4/6 is 8/30ths.” The student who shared this had gotten the answer “right” but he wasn’t satisfied. He knew how to do the problem but he couldn’t explain why it worked. Sure, you could multiply the numerators (top number) then multiply the denominators (bottom number) but why did that work?

The question opened up a big conversation. I asked the students and about half felt sure that multiplying the numerators and multiplying the denominators would always work to multiply fractions but the other half weren’t sure. I asked if anyone had a counter example of when it didn’t work.

A child raised her hand, “There’s one thing where you multiply the top number by the bottom number.” I pushed gently, “When does that work?” “Um….I don’t remember what thing it is but that’s how you do it and it is multiplication.” This is very common – she had learned a procedure — but she hadn’t yet mastered when to use it or how it worked. It was “something you did.” I suggested that since the details weren’t clear, it wasn’t a counter example. (And I quickly assured her that she was remembering an algorithm for cross multiplying and that we would work with it soon.)

We backed up and drew some pictures of simpler examples. We talked our way through a decomposed version (2×4)x(1/5 x 1/6). We kept at it until every kid was able to say, “I see what we’re doing. It will always work! I can explain why.”

In my work with the 5th graders this year, I have emphasized that “math makes sense.” And, if something we are doing in math doesn’t yet make sense, they have the responsibility both to themselves and the other kids in the class to ask, “WHY?” If we just memorize the “how” of a math problem, we quickly run out of memory space for how to compute each and every kind of problem. Instead, I want students to really understand how number are interacting and what they mean.

The very next day, I came in from lunch to find a group of animated students at the whiteboard. One student had our fraction magnets out, another was drawing a number line with fractions. There were several more fraction representations being drawn. When they saw me they pounced, “Which one do you think is bigger? 4/10 or 5/12?” One kid offered, “Tenths are bigger pieces so it seems like that one should be bigger” another countered, “But each one is one piece short of a half and a twelfth is a smaller piece to be missing so that one is bigger.” I asked if I could just listen for a while and the students talked back and forth. The child who had initiated the debate had been told that 5/12 was bigger but just didn’t believe it yet, “I know which one is right but I don’t see why!!” she exclaimed. She wasn’t satisfied until the child with the fraction magnets built both fractions. That she could believe.

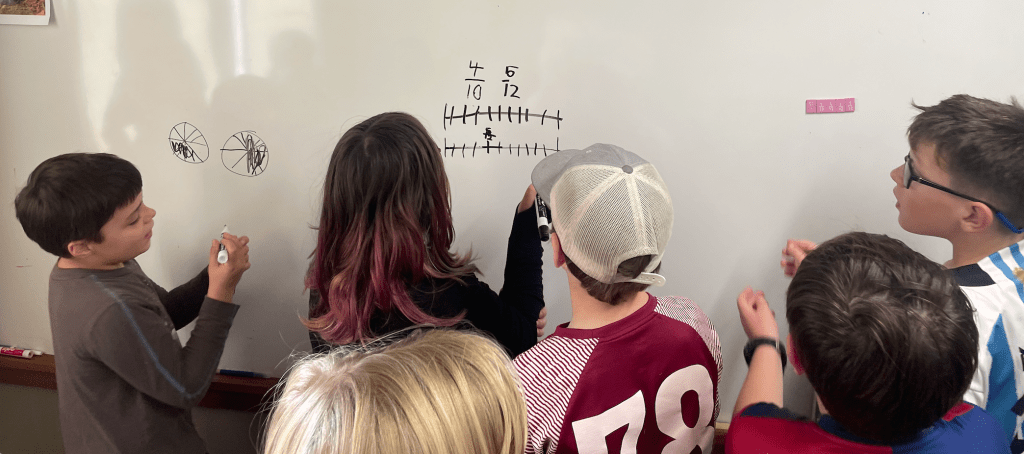
Building a math community takes time. Students have to be willing to wonder and struggle and question and fail in front of each other. Every day I work to celebrate the questions and the confusion. We seek the “OH!” moments of clarity that are so powerful but can only come when doesn’t understand then fights to figure things out. And, eventually, you get to enter a room and find your students spending their free time debating math. It doesn’t get much better.